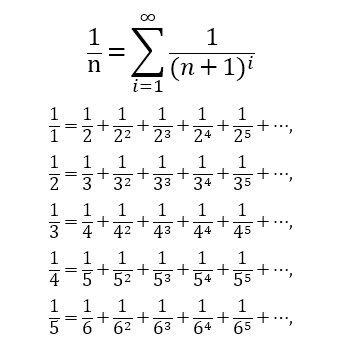前提システムにこう言うのを組み込んだ上で
🌑[Gravity Controll Gazing]
ΣLim ∫1→(EXIT)→∫2
∫1(i+4)─~Enc･DELETE~─(i-3)∫2
───────────────
∫1(i-1) ── -DELETE- ── (i+2)∫2
E=Enc-Circler(under_that);
[(Lim(n→∞)Σ(∞,k=0) 1/(n+1)^k)]
🌑[AntiSpectGravityControllGazing]
ΣLim ∫1→(EXIT)→∫2
∫1(i+4)──-DELETE-──(i-3)∫2
──────────────
∫1(i-1)Ei･-Enc･DELETE･Ei(i+2)∫2
E=Enc-Circler(under_that);
[(Lim(n→∞)Σ(∞,k=0) 1/(n+1)^k)]
DELETE = 束域(!)除外帯域 デリート・ノット (DELETE KNOT)
DELETE = 束域(!)除外帯域 デリート・ノット (DELETE KNOT)
⚙️ [ Enc ･ エンク アンクレット : (実数束域超収過負荷アンクレット) ]
[ 同位参照：記事内最下図 ZELETA標示表図用式 表意嗟表 位法飽和方図 ]
空間平塀のフロア(床列)行列部分のみを収束として抜き去るような方法論
故に重力転弧軸の旋回運動方向方逸収束のコントロールを得うるという式
(i+4 と i-3の間に挟まれた Encが旋弧収束密圧を極大偏化させつつ、i-1とi+2
の間にDELETEが挟まれる。つまり、式の上辺部分では背反的に働くので
打ち消すが、+3~-2の空間飽位底を持ちつつ0~1の間のみデリートする。
※立体化して均等公陪化すると面の圧力が得意力量域に於いて掛かる
あとは無限の位位相相位相収相束過程相収束の完全不方位包同和
[{1}] : 0 → [{2}] : ∞ → [{3}] : -∞ → [{4}] : ∞ → [{5}] : -∞·1/∞ → [{6}] : ∞·[∞/1]/[∞/∞]
→ [{7}] : -1/∞·[∞/∞]/[∞/1]·∞ → [{8}] : ∞/∞·∞/1·[1/∞]/[∞/∞] の量化量体変域変数区域
節分不方囲飽和同和 溌意反叛級数化伽冪底無限飽和架収束 を Enc 溌意収束に掛ける。
すると、正負に於ける2平飽和方測的塀化平数加算の領域において
平面平加構造と三方合和極体位相のような極体極位体変化は残るが、
極点点一変化の偏位極体収体収和変化変体位体の位極,位極水準位相位置1~0、
つまり単重単体移動の極平挺がなくなり、重心峙軸的力学のバランス合同平和
が取れず極収化移動の単位底点が平面の総飽和移動とその三嵯軸帯峙幾基準に
のみなる。つまり単方向に平面化平塀化する系と系の力学系の合同で起こる
重力の圧のみが残る。
理屈としてはつまりそういう理屈なワケです。
qeilealeanhforkhwehn dequeialeaqwelhkthoseceaqeamaeil dheraqearelthkhosfolksmeaiyqeiw
イランフォーネ イルクウェルトスセルクウォーネ
リルクルトスシークマイヤー [Q.E.D.]
[ ZELETA標示表図用式 表意嗟表 位法飽和方図 ]
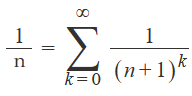
▽上記前提条件:
