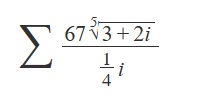
空間幾何の記事と参考にしながら、平方展開、立方展開を頑張って。
4象限平方化.8象限立方化を±合わせて下の通りにするとする、
[!?][!!?][!!?!][!?!!][!?!!][!?!!][!?!][!!][!?][!!?][!!][?!][!!?][!!][!?][!!][!!?][!?!!][!][!?][!?!][!!][!!?!][!!!][!]
5076通りくらいのパターンが出来るとする、これを元に上の虚元方程式を方坪展開
🫧 新しい daa't 27[3^3] - 16[2^4] = 11 三冪化型もちゃんとやっておこうか
🦄 完☆全☆勝☆利したRiotTheSplitter(Unicorn系男子) ニ冪と三冪の交対応はこれで
T3TA:TheorumThreeTimeArrows &&
ANOTHER THINGS THREE TIME ARROWS
これをベースに10軸展開した後、
T3TA:Theorum - 3 - Three - Time Arrows : Mesfa Melfa &&
Mesfa Lumina Gold Star [MesfaTrine &&More TheorumLimit]
で四体安定させたら11に至る、
T3TA4:Theorum - 3 - Three - Time Arrows For Leaves
これを以てその11自体を浮遊させ鋭化射出させる。12Trine
2i(1k) → 4i(2k) ベースド √8:{ √4i:Tiger && √4i:Tiger }
四回繰り込むとクロスウェンナード式積った場合
最後の四回目で残った1とi4=1が2隔乗離帯積になるので
完全に1で静止。ハイパーステイシスステートメントスチュード
これを以て上記12Trine自体を完全に1なる静的化。13Quareltive
これを以て13Quareltiveまでを0~∞開放。14Arraiviel

15Parabel ここまでで自由遊化 

777と666を下の記事の方に書いたものと対応させ、16Episode~17Arabelを描く
![]()
![]()
![]()
![]()
![]()
![]()

18Revels 下の888と対応
19Crinel 下の999対応
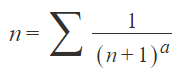

20Graudhia x,y,z に冪化繰り込み参照完全次元法定フリンジング
ヘルメス・トリスメギストス理論 + クォート 3冪化幾何束式も加え
✡️ 魔法陣法:3乗冪底 TRINO PILAMIDHMIDHONN EXETOR



21~22 GazerHaut && GailAnotherHaut
23 RezhaDhiahadekazha
Σ(0→∞→-∞→∞→±0→±+∞
→∞・∞/[1/∞]∞→∞・[1/∞]∞/∞[1/∞]∞
→∞[1/∞]・[1/∞]∞/∞[1/∞]∞・∞/∞[1/∞]
→∞[1/∞]∞・∞[1/∞]∞/∞[1/∞]∞・∞[1/∞]∞/∞[1/∞]
i-idiotzha ∫(z~a)
count d1 Criminal Curve 2π/√8 →π/8 d2
count d1 Curlmolasor Curve 4π → d2
d1 to d2 [dmax: d(1) to d(2).......d(dmax)]
dmax to d(l) decrimentum l; d(dmax -l )
{ ∑ 67·5√[3+2i] / [1/4]i }
{ 2i : -3si2 : 5li4 [≡:∮:∪] }
{ 4li : 8li : -5li [*Σ:≡:**∽]([!?][!!][!?][!?!][!?][!!]) }
{ 8i : -7i : 6i : 5i [ [xm:xn:xl:xx] : [∫:≡:Δ:∮] :: ∮{[!?][!!][!?]∪[!?][!!]∩[xn:xx:xm:xl(segment∫[2~4]::add:([!?][!!][!?][!!][!?!][!!][!]))]}}
{{ 2i : -3si2 : 5li4 [≡:∮:∪] }
{ 4li : 8li : -5li [*Σ:≡:**∽]([!?][!!][!?][!?!][!?][!!]) }
{ 8i : -7i : 6i : 5i [ [xm:xn:xl:xx] : [∫:≡:Δ:∮] :: ∮{[!?][!!][!?]∪[!?][!!]∩[xn:xx:xm:xl(segment∫[2~4]::add:([!?][!!][!?][!!][!?!][!!][!]))]}}
2i : 3i : -5i : 9i : 10i : -11i : 12i [∫:∮:*Σ:*⊕:∩:∫ :≡] }}
24 LhazhaclaizheRazen 🕶️ BreakOutMomentum!!な理論
i-idiorodhiaを上記全てに加えて完全極開
💠 DotTears──🔷DisGrasen[10][10][10] (sert philler x,y,z)
◆DotTears──DisGrasen[10][10][10] (sert philler x,y,z)
[x4:2][2^3][3:2n]
[y9:3][3^2][2:3n]
[z25:5][2+3][5:n]
[x][y][z]:[15][24][30]
SigmaArisen(d:[n]->d.x.y.z)
{[10]:[x4:2]},{[10]:[y9:3]},{[10]:[z25:5]}
をベースに引数(システム平面形示上実数 philler)代入可
x,y,zは転回可能,完全に制御可能な意思決定的能動システム数学系
◆DignoNine─Trino[9][9][9] Forge F
{[3i][2i][1i·i(-i)][-1i][i·i]}
{[3i][2i][1i·i(-i)][-1i][i]}
{[3i][2i][1i·i(-i)][-1i]}
Sigma Rate.F<DignoNine>(√[2√2·2if^2]^2);
F(SetPart:ToEnd:DignoNine)
Lim Int Deal Σ F[9/11]&&F[1/10]
Lim Str Dead Σ F[1/10] , Σ √4·2F[1/10i , 1/10i]
◆EIGHT THE SAN {...:[[(8)][(8)][(8)]]:...}
[(8)]:{[(mote) 4[ins](2i-[ins])^2]}
$K:[Kaunta:K]
(mote):{[(THAT)<-*(if){(Do #Intentionaly) Look.Val-Alt.K]}
(ins):{inscriber-Nested Look.i-'!'(cont∮[1K:[1[4i(i-idiot)]])}
*on[4i:<-Fact(add.K(n)])]) (molt):{[(mote)->this<-(ins)]}
IntensionalAddtivitySeeingCurrentDictionary
WholeSigma{[(8)][(8(molt))][(8(molt)^(molt))]}
Math-DimensionalShift-IntegrateSeeing
CurrentalSpaceViewingSite-Dictionary
:_->Look
◆Reach7-Triset/ignorthia[(system)i-idiot∫]
◆DoubleCladShaft[666/777][(import)ZETA EXFUNCTION]
[(Boot)]Σ[67·(5)√(3+2i)]/[(1/4)i]
[(FreeBoot):(CRUCK)]
[(CRUCK)<=('IF' AND 'OR:∫')]
[R; [7]:[(2+0i)^3]
[(CRUCKS)<=('CLOSE' OR 'INTEGRA')]
CLOSE:{[ShortDruggen()]:[∫(0+i)∮(1+2i)∫]}
INTEGRA:{[IntegtralShort()]:[∫(i-1)──(i-0)]}
──────────────────────
{([7]+7)+([7]x7)+(-7[7])}[(CRUCK)]
[7]6·5i√79·8i[(CRUCK)]20√6+4i[(CRUCK)]
6+6x6(+5x5)[(CRUCK)]5√3+2i[(CRUCK)]1/4i
Σ[67・5√3+2i/(1/4)i]
Σ{[8√(2√4i)・1・7√(i√i)][(!(n+1))^3]}
◆Reach7-Triset/ignorthia
この数式基準イメージしてたら
あまりに自由自在に数幾何旋転
時間軸進行方向へ伸びる動態
としての幾何空間が持てる
◆DoubleCladShaft[666/777]
666onSET
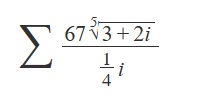
36(6^2)+27(3^3)+(2^2):67
5√3+2i:5^5==5i
1/4i
つまり、この式は3·2=6と3,2のn^nの和の差を
割った分の差を求めて底素虚元に至る式だった
あるので底素となる虚数の虚元……としか表現……
……出来てしまったのです。……なぜか、あの時……。
展開については:これ能動化Activate
(ai-b)^(Σthis) THIS:[ ∑ { [ (67 · 5√3+2i ) ] / [ (1/4i) ] } ]
aとbは後ろ方,右項の方の ∑ には
引っ掛けないでください。台無しになるんで
この数式(666)と(777)両立両手持ちで使うと飛びます。